Navigation
We accomplished the terminal motion of a stacking task with a UR-10 manipulator in MATLAB/Simulink.
This is a project of ME385(Robotics) of SJTU. In industrial scenarios, manipulators are always deployed to carry heavy things and stack them in a specific order. We take the UR-10 manipulator as an example, setting up a stacking task and studying its dynamics, control, and planning.
Dyanmics and Kinematics
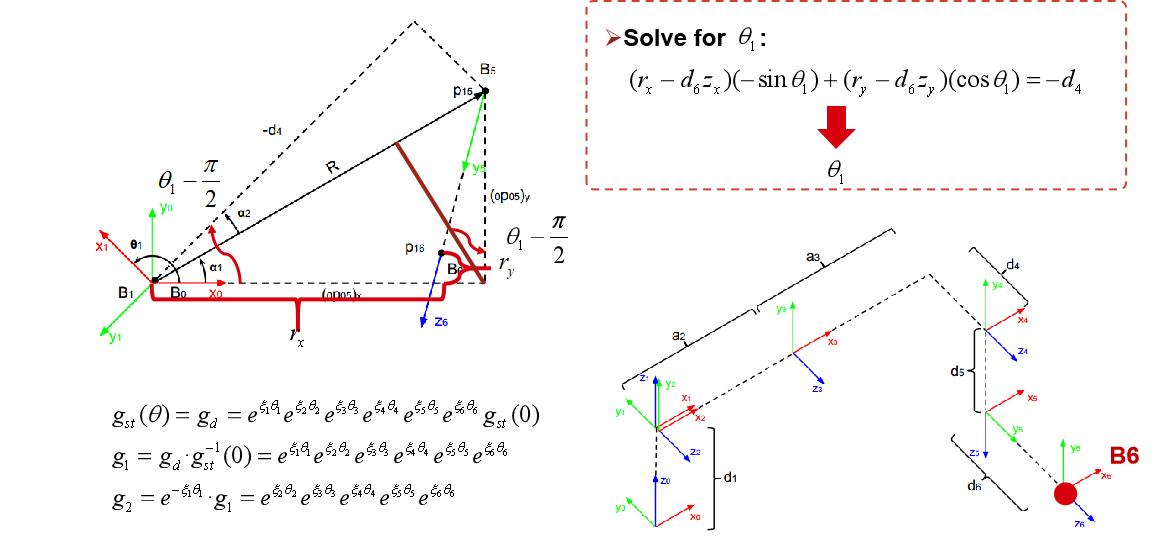
Based on the product of exponentials (POE) approach, we developed the kinematics of UR-10, and verified our method with MATLAB/SIMULINK robotic toolbox.
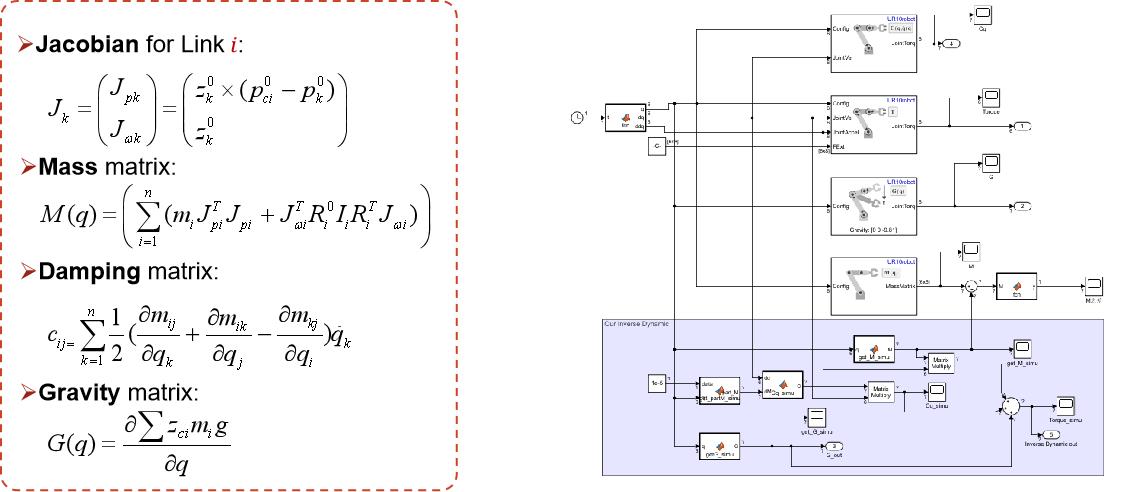
To control the manipulator, we need to establish its dynamics. In this project, the dynamics in joint space were derived based on the Euler-Lagrange formulation to enable a computed torque controller. And we also tested its performance with SIMULINK.
control
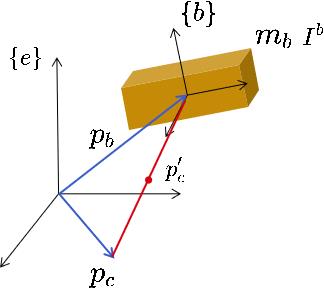
Cargo is attached to the end of the manipulator during the stacking process. Thus, the manipulator's mass matrix must be modified to control the manipulator when it is loaded. We modeled this based on the simplification of the inertia matrix and developed a controller. The computed torque controller** was designed as: \begin{equation} u(t) = M(q)(\ddot{q}_d + K_p \tilde{q} + K_d \tilde{q}) + C(q,\dot{q})\dot{q} + G(q) \end{equation} with compensation adjusted by parameters \( K_p \) and \(K_d\).
Path Planning
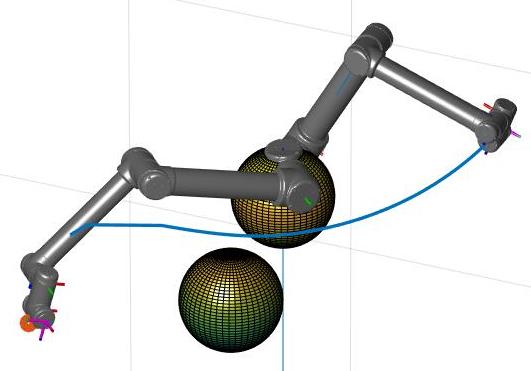
To avoid collision with fixed environmental obstacles, we implemented a path planning algorithm to calculate a short and reasonable path for the manipulator in the joint space. Meanwhile, self-collision can not be ignored. To tackle this, We designed an artificial potential field (APF) and defined the repulsive force between obstacles and links, links and links. To escape from local minima, we utilized a tracking back strategy. And we also used low-pass filters to smooth the calculated path.
Trajectory Planning
After generating control points of the path in the joint space, the shortest time trajectory planning was conducted with sampling first to reduce the dimension of the following optimization problem. Based on cubic splines, the problem was formulated as SQP procedures: $$ \min T = \min_{\Delta t_j} \sum_{1}^n \Delta t_j $$ and it was solved with MATLAB fmincon function.